Counterfactual Explanations without plausibility term, and those including a plausibility term such as KDE, GMM or kNN.Abstract
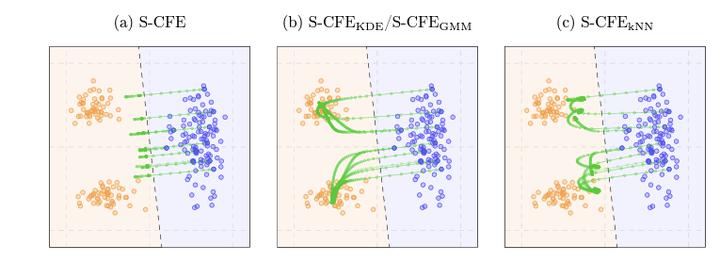
We study the problem of finding optimal sparse, manifold-aligned counterfactual explanations for classifiers. Canonically, this can be formulated as an optimization problem with multiple non-convex components, including classifier loss functions and manifold alignment (or plausibility) metrics. The added complexity of enforcing sparsity, or shorter explanations, complicates the problem further. Existing methods often focus on specific models and plausibility measures, relying on convex l_1 regularizers to enforce sparsity. In this paper, we tackle the canonical formulation using the accelerated proximal gradient (APG) method, a simple yet efficient first-order procedure capable of handling smooth non-convex objectives and non-smooth l_p (where 0 <= p < 1) regularizers. This enables our approach to seamlessly incorporate various classifiers and plausibility measures while producing sparser solutions. Our algorithm only requires differentiable data-manifold regularizers and supports box constraints for bounded feature ranges, ensuring the generated counterfactuals remain actionable. Finally, experiments on real-world datasets demonstrate that our approach effectively produces sparse, manifold-aligned counterfactual explanations while maintaining proximity to the factual data and computational efficiency.